建造环境课题组王延敏博士在中科院一区期刊《Applied Energy》（JCR Q1， IF= 11.4）发表了研究论文，采用聚类和回归方法研究集中供热建筑室内温度的日变化规律。

 

1. 题目

Analyzing daily change patterns of indoor temperature in district heating systems: A clustering and regression approach

集中供热系统室内温度日变化规律分析：一种聚类和回归方法

2. 作者

Yanmin Wang（王延敏，天大/大连海心），Zhiwei Li（李志伟，天大），Junjie Liu（刘俊杰，通讯作者，天大），XuanLu（鲁轩，大连海心），Laifu Zhao（赵来福，大连海心），Yan Zhao（赵岩，大连海心），Yongtao Feng（封勇韬，大连海心）

3. 研究亮点

l基于偏差的观测矢量表示每日室内温度模式。

l聚类分析揭示了室内温度日变化的不同模式。

l使用k-means算法（DBI=0.63）实现了最优聚类有效性。

l通过不同的特征观察到集群之间的显著差异。

l使用MNLogit模型评估不同特征对聚类的影响程度。

4. 研究背景

测量集中供热建筑的房间室内温度不仅可以评估热舒适性，更重要的是一种为集中供热换热站提供反馈控制的有价值的方法，基于物联网采集室内温度可以实现“按需供热”的新型智慧供热控制模式。国内许多供热企业按2~10%的热用户比例安装了室内温度采集设备，如何利用采集的大量温度数据实现智慧供热需要解决提取室内特征温度的难题。图2展示了2022-2023供热季一个室内外温度趋势的例子。（a）是两个室内温度采集设备采集的数据，（b）是同一地区的室外温度数据。很明显，来自两个设备的室内温度呈现不同波动。尽管偶尔会出现同样的波动，但总体趋势并不一致。此外，与室外温度趋势相比，室内和室外温度之间没有明显的线性关系。

 

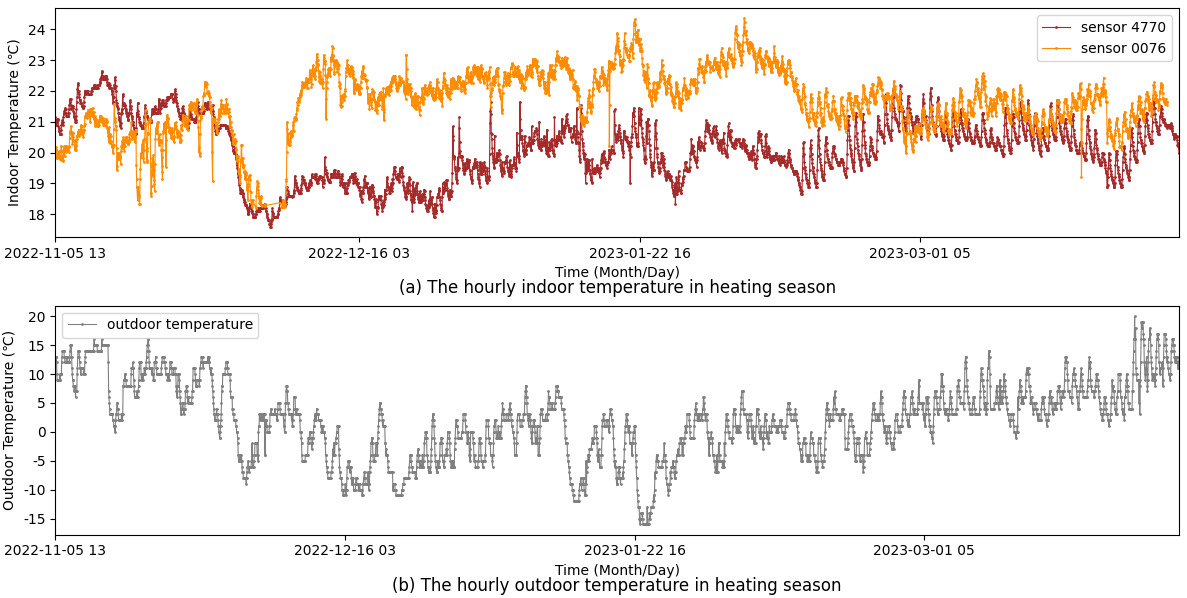
Fig. 2. Example diagram of indoor and outdoor temperature trends during the heating season.

图2 全供热季室内外温度趋势示例图

以往对室内温度特征的研究大多从空间和时间分布模式的角度，总结了不同建筑位置和时间点的室内温度特征，但对室内温度本身的变化模式，如变化趋势和波动的研究相对较少。以往的研究也识别了影响室内温度的影响因素，包括天气条件、供热参数、建筑特征和热用户活动等。当天气条件发生变化时，供热企业会调整供热参数以保持室内温度稳定。然而，即使在相同的天气条件和供热参数下，室内温度也可能因建筑物特性（如用热面积、建筑年代和墙壁厚度）和热用户活动（如居民人数、在家时间和突然开窗行为）的差异而发生变化。这些研究的重点是调整不同的参数以保持室内温度的稳定，对各种因素的影响程度缺乏定量分析。

在集中供热系统中，聚类是常用的一种数据挖掘工具。一些研究根据其独特特征对热用户进行分组，更多的研究对热负荷的日变化模式进行了聚类分析。为理解聚类结果与特定特征的关系，很多研究使用算法模型来分析影响聚类结果的因素。

综上，室内温度是热用户热舒适性的重要指标，受多种因素的影响。了解影响室内温度的关键参数对于实现集中供热系统的精确控制至关重要。由于位于同一栋建筑物或同一个换热站，从室内温度的角度来看，热用户之间没有本质的区别。这些研究启发我们可以从日变化模式的角度来分析室内温度。本文采用聚类方法对室温日变化模式（DTP）进行了研究，并分析了不同因素的影响程度。

5. 主要成果

5.1 提出了研究流程

本研究分为五个步骤，如图3所示：

（1）收集了多个热用户的室温数据及对应的换热站运行数据、天气数据和热用户数据；

（2）对原始数据进行预处理，包括异常值、常数值和缺失值检测及处理；

（3）提取DTP的代表性模式特征：定义了一个24小时观测矢量来代表每日室内温度曲线，并使用实际值和目标值之间的偏差来放大信号强度；

（4）对提取的DTP进行聚类，分析每个簇的数据量分布和典型特征；

（5）分析了各种因素对聚类结果的影响程度。

 

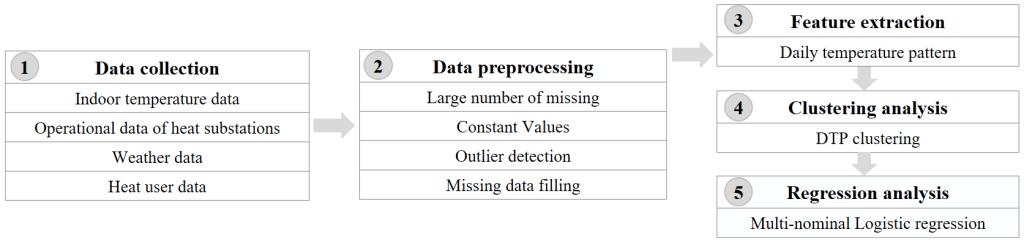
Fig. 3. Flowchart for clustering DTP.

图3 本研究的处理流程

5.2 试验对象选择

本研究的试验对象来自中国东北的一个真实的集中供热系统，共有供热面积121万平方米， 1.05万户，22个换热站。初始选择了917个室温采集设备，经过数据预处理后，剩余397个，其安装位置如图5所示。

 

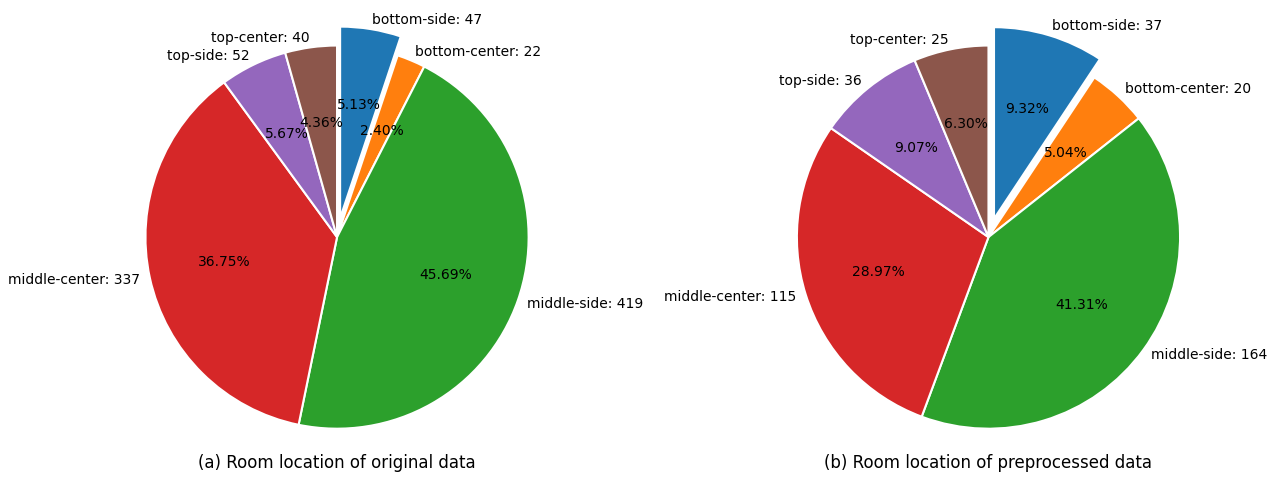
Fig. 5. Location distribution of rooms with indoor temperature sensor installed.

图5 安装了室温采集设备的房间位置分布

 

5.3 试验数据收集

试验数据取自2022年11月5日到2023年4月5日，共152天。其中节假日49天，包含春节、周末；工作日103天。

室温数据每30分钟采集一次，共1,397,489条；换热站运行数据包含10个特征，每小时采集一次，共80,256条；天气数据包含7个特征，每小时采集一次，共3,648条；热用户数据包含4个特征，共397条。

室温数据经过处理后，获得了54,384个代表每日室内温度曲线的观测矢量，其中37,454个在工作日，16,930个在节假日。

 

5.4 聚类算法选择

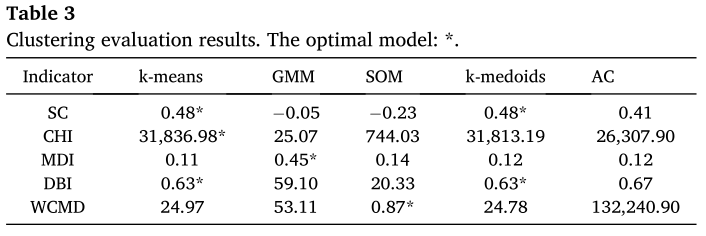
为选择最优的聚类算法，本研究选择了五个典型的聚类算法，包括k-means（K均值聚类算法）、GMM（高斯混合模型）、SOM（自组织映射）、k-medoids（k中心聚类算法）和AC（层次聚类算法）。然后使用五个评价指标来评估聚类的有效性，包括SC、CHI、MDI、DBI和WCMD。在所使用的五个评估指标中，有三个将最优聚类模型指向了k-means。因此，考虑到所有评估指标的综合性能，k-means被认为是本研究的最佳聚类模型。具体结果见表3。

 

 

5.5 聚类的数据量分布

使用SSE（误差平方和）来计算聚类的数量，结果表明，最优的聚类数量为4。每个簇的数据量分布如图6所示，结果表明工作日和节假日都表现出相似的特征。簇1是最大的一组，占观测总数量的41%以上；簇2是第二大组，占观测值的33%以上；簇4是最小的组，不到总观测值的10%。

图6 (c)是每日的聚类数据量分布，结果同总体的数据量分布一致。可注意到的是，在供热季的中期，簇4的数据量有显著的增加，每个簇的数量趋近均衡。这种现象是由于这个期间室外温度降低，供热企业调整了供热参数导致的。

 

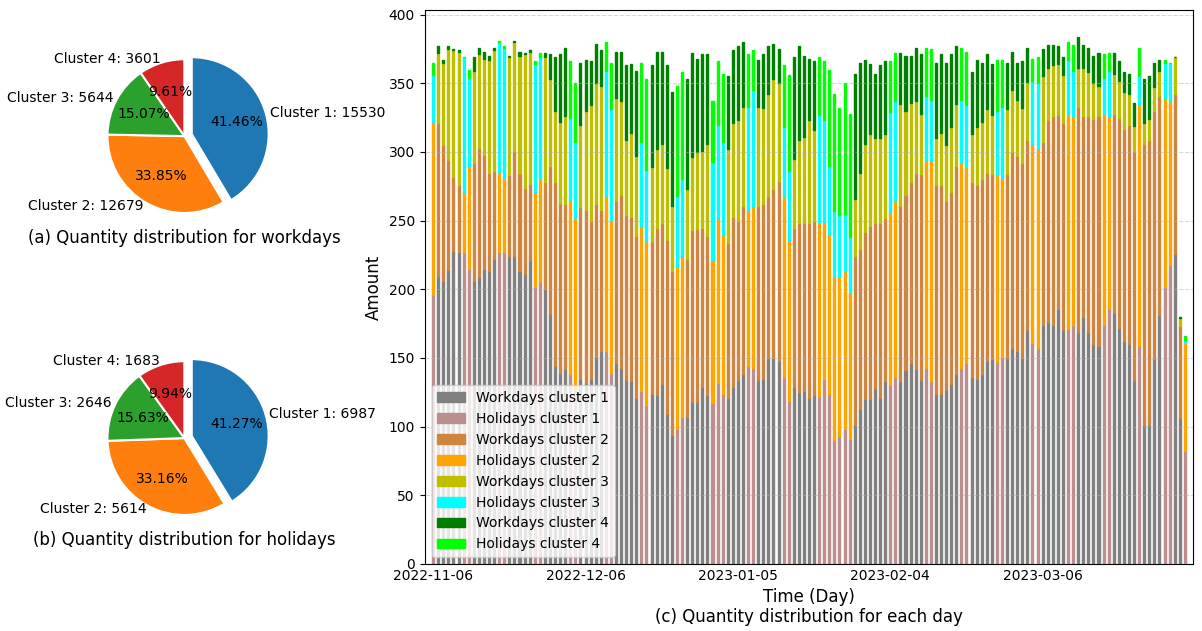
Fig. 6. Quantity distribution for clustering with =4.

图6 聚类数量为4时的数据量分布

 

5.6 每个簇的特征

图7是每个簇在节假日和工作日的日室温曲线，其中粗线为质心，细线为代表性明细数据。总结每个簇的特点为：

1）簇1：在四个簇中，波动相对较小。最低质心出现在大约8:00，其值为10.76%；最高质心出现在14时左右，达到12.43%。下午下跌后，18时至20时略有反弹，18时为11.96%，20时为12.03%。最高点和最低点之间的偏差为1.67%，所有时间点的平均值为11.61%。

2）簇2：与其他簇相比，该簇的曲线陡峭度排名第二。在大约7:00观察到最低质心，其值为-2.33%；最高质心出现在14:00左右，达到-0.07%。最高点和最低点之间的偏差为2.26%，所有时间点的平均值为-1.22%。

3）簇3：在四个簇中，具有最平滑的曲线。质心没有显著变化的明显时间点。最低质心周期从8:00延长到9:00，值为25.82%；较高的质心周期出现在13:00-15:00，持续时间较长，为26.66%。最高点和最低点之间的偏差为0.84%，是四个簇中最小的。所有时间点的平均值为26.22%，是四个簇中最高的。

4）簇4：该簇中的曲线在下降和上升过程中都表现出显著的振幅，表明上升和下降都很陡峭。最低质心周期持续两个小时，从6点到8点，数值为-19.42%；在14:00观测到最高质心，值为-16.69%。最高点和最低点之间的偏差为2.73%，是四个簇中最高的。所有时间点的平均值为-18.03%，是四个簇中最低的。

尽管簇2更接近目标值，但对热用户的舒适度并不友好。簇3的波动最小，但室内温度远高于目标值，这很容易导致更高的能耗。簇4远低于目标值。因此，簇1是实际操作中的最佳目标。

 

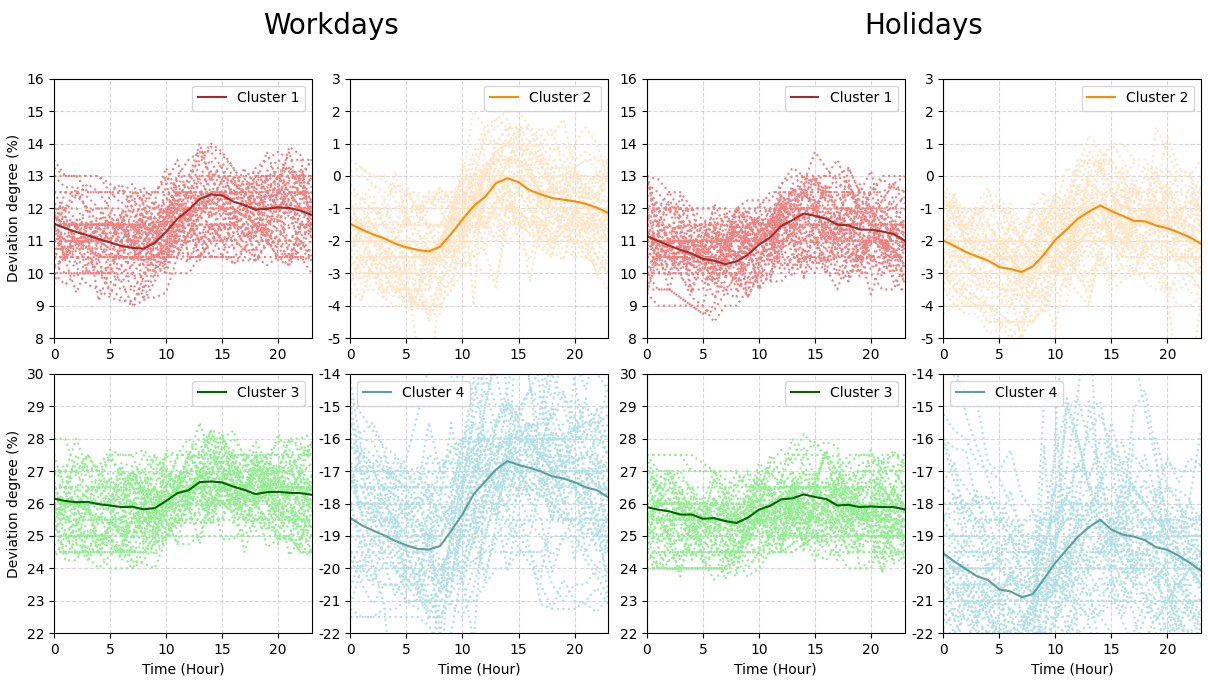
Fig. 7. Daily temperature patterns for clustering with =4.

图7 聚类数量为4时的日室温模式

 

5.7 所有特征的回归分析

使用MNLogit对所有特征进行了回归分析，计算了四个解释性统计指标，分别为estimated coefficient（估计系数）、standard error（标准误差）、odds ratio（比值比）和P-value（统计显著性）。选择簇1作为参考簇，并将所有其他簇与之进行比较，工作日的计算结果如表4所示。

 

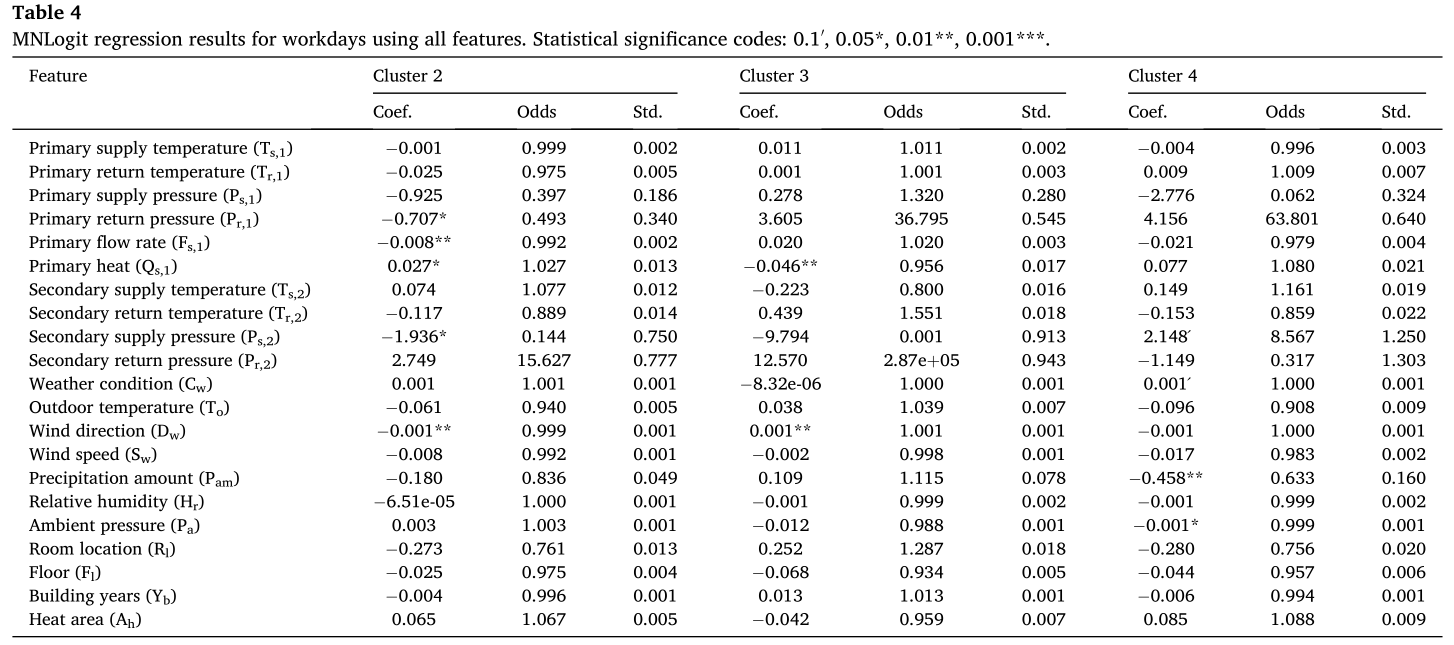
分析结果表明，供热参数、天气参数和热用户参数都在决定聚类结果中发挥了重要作用。供热参数中具有显著影响的特征包括一次供水压力、一次回水压力、二次供水温度、二次回水温度、二次供水压力和二次回水压力。影响显著的热用户特征是房间位置。

 

5.8 部分特征的回归分析

为了进一步探索各种特征对聚类结果的影响，选择了上述计算过程中影响较显著的一些特征，以簇1为参考簇，计算了四个解释性统计指标，工作日的计算结果如表6所示。

 

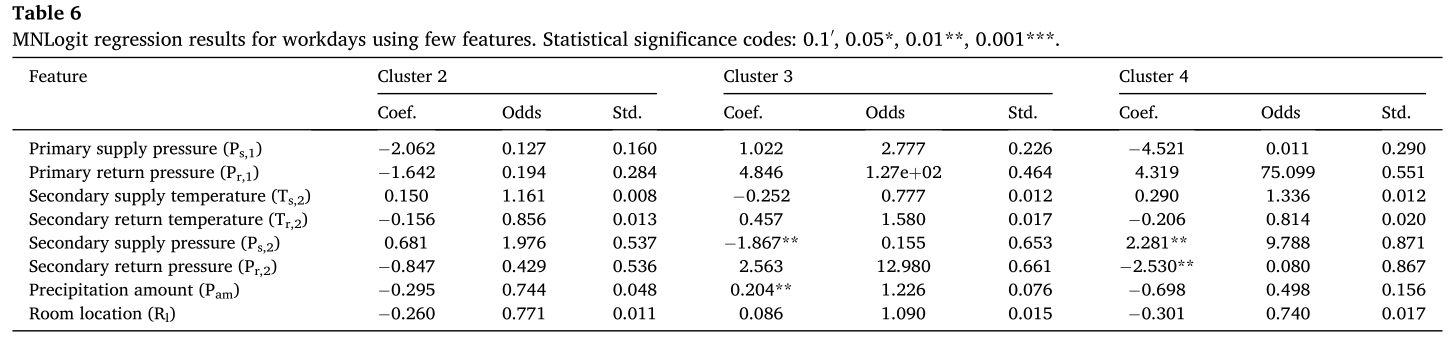
分析结果表明，对于工作日和节假日，最显著的特征是二次供水压力和二次回水压力。对于工作日，他们在簇4的置信水平为99%；在节假日，他们对簇2和簇4的置信水平为95%。

总之，对聚类结果有高度影响的主要特征包括一次供水压力、一次回水压力、二次供水压力和二次回水压力。特别是在工作日的一次回水压力，在节假日的二次回水压力，影响更为显著。

 

5.9 结论

揭示室内温度数据中隐藏的信息是一个有意义的话题。本研究使用聚类方法来分析室内温度数据，主要结论为：

1）使用实际值和目标值之间的偏差作为基本特征，构建了一个以天为单位的24小时观测矢量，可以有效地捕捉并反映DTP随时间的变化趋势。

2）采用k-means方法对DTP进行聚类，使用五个评价指标将k-means聚类的性能与其他四种有代表性的聚类方法的性能进行了比较。结果表明，k-means方法优于其他聚类方法，工作日和节假日的最优聚类数均为4。

3）分析了各簇的数量分布和典型特征，考虑了每个簇的数量、质心和细节之间的距离、质心值的范围以及质心的每日趋势。簇1数据量最大，簇4数据量最小。尽管每个簇的趋势大致相同，但波动幅度和与目标值的距离存在显著差异。簇1是实际操作中的最佳目标。

4）使用MNLogit方法对聚类结果进行回归分析，以簇1为参考簇计算解释性统计指标。分析表明，一次供水压力、一次回水压力、二次供水压力和二次回水压力对聚类结果有很大影响。尤其是工作日的一次回水压力和节假日的二次回水压力对聚类结果的影响最为显著。

 

本研究结果对提高集中供热系统的调控效率具有现实意义。聚类模型确定了满足热舒适性要求的室内温度的最优日变化模式，回归模型分析了影响这种模式的重要特征及其影响程度。这些研究有助于实现换热站的更精确调节，从而提高整个系统的性能。

 

文章引用格式：

[1] Yanmin Wang, Zhiwei Li, Junjie Liu, Xuan Lu, Laifu Zhao, Yan Zhao, Yongtao Feng. Analyzing daily change patterns of indoor temperature in district heating systems: A clustering and regression approach. Applied Energy 2024;358:122645. 

原文链接：https://www.sciencedirect.com/science/article/pii/S030626192400028X?via%3Dihub

 

 

稿件编辑：王延敏
稿件审核：刘俊杰、田媛、于欣宇